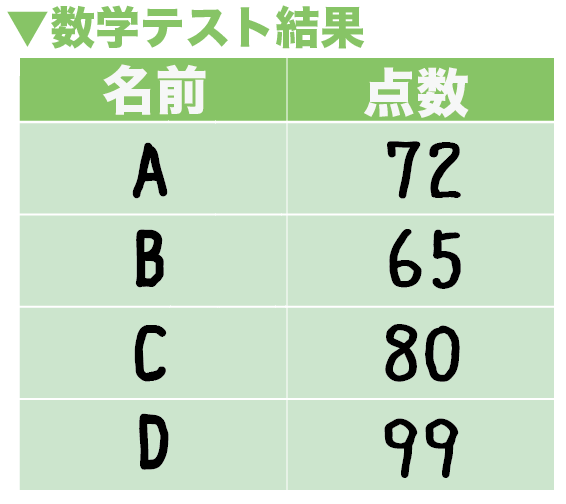
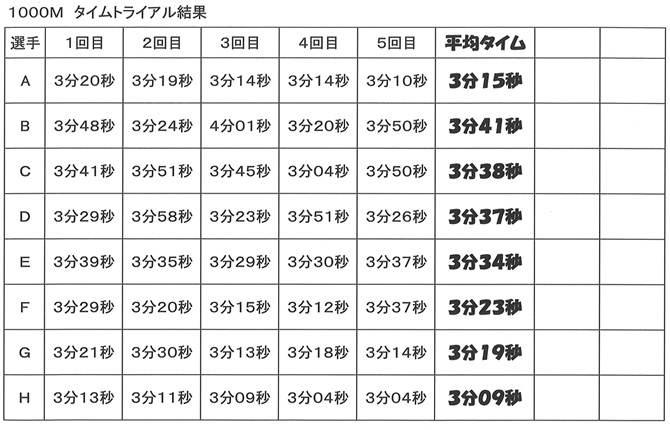
このノートについて ゆう 資料の分析と活用 相対度数 近似値 有効数字 平均値 中央値 最頻値 階級値 データ データの分析 平均 メジアン モード 標準偏差 分散 相関係数 ヒストグラム このノートが参考になったら、著者をフォローをしませんか? 気軽に 7章資料の活用p17章 資料の活用 2年 組 番名前 ルーラーキャッチって、どんな遊び??? 落下する定規を何㎝のところでつかめるのか?を調べる遊びです。 →詳しくは、1年生の教科書232ページを見てね! 1.まずは、平均値で比べてみましょう。第1学年 7 資料の活用 知識・技能の習得を図る問題 年 組 号 氏名 練習問題④ 1 1500 mが次の位までの測定値のとき,この測定値を有効数字で表しなさい。 3(m)と表す
資料の活用の問題で 中央値 最頻値 平均値の3つの問題の解き方教えて Yahoo 知恵袋
数学 資料の活用 平均値
数学 資料の活用 平均値-キーワード 新学習指導要領,中学校数学,資料の活用,度数分布表,代表値,有効桁,10n 1 はじめに 平成24年度に実施される中学校の新学習指導要領4 の数学では,従来の領域「数量関係」が2つに分かれて, 新領域は「数と式」,「図形」,「関数」,「資料の活用」 こまめに復習を 階級 度数 度数分布表 相対度数 中央値 最頻値 メジアン モード 平均値 数学 中学 データ データの分析 平均 標準偏差 分散 相関係数 ヒストグラム math このノートが参考になったら、著者をフォローをしませんか? 気軽に新しいノートを




中学数学 資料の散らばりと代表値
中学数学最頻値(モード)の求め方がわかる2ステップ 最頻値(モード)の求め方がわからない!! こんにちは!この記事をかいているKenだよ。ドタキャンはきついぜ。 最頻値(モード)の求め方 を知っていると便利。 資料と活用の問題がとけるし、 中学数学中央値(メジアン)の求め方がわかる3ステップ 中央値(メジアン)の求め方がわからない?? こんにちは!この記事をかいているKenだよ。チャーハン炒めまくったね。 中学数学の資料の活用では、 中央値(メジアン) を勉強するよね。平均値,中央値,最頻値の求め方といくつかの例 データ群の特徴を一つの数値で表したものを代表値と呼ぶ。 代表値の中でも平均値,中央値,最頻値が有名。 平均値,中央値,最頻値の意味と計算方法を解説します。 いくつかの具体例を通じて
Lesson 47 代表値-平均値・階級値・中央値・最頻値 第7章 資料の活用 <<L47 代表値平均値・階級値 の解答消去 L48 近似値・有効数字 の問題に進む>> 練習問題1数学科学習指導案 4 単 元 名 「資料の活用」 5 単元について (1)教材観 本単元は,中学校学習指導要領第2章第3節 第1学年 D 資料の活用 内容(1)「目的に応じて資料を収 平均値を求めることはできたけど,それだけで中1数学『資料の整理と分析』のところでの平均値の求め方は2パターンです。 一つは小学校のときからのおなじみの平均値の求め方です。 平均値: 個々の資料の値の合計を資料の総数で割った値 もう一つが、度数分布表から平均値を求める求め方です。
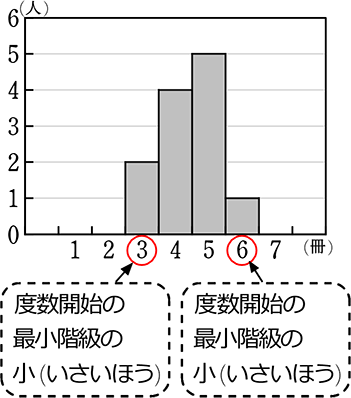
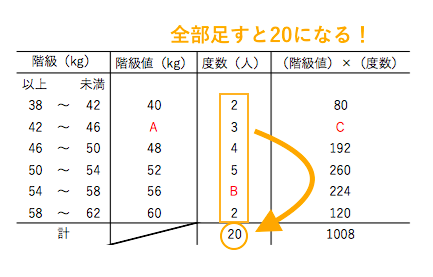
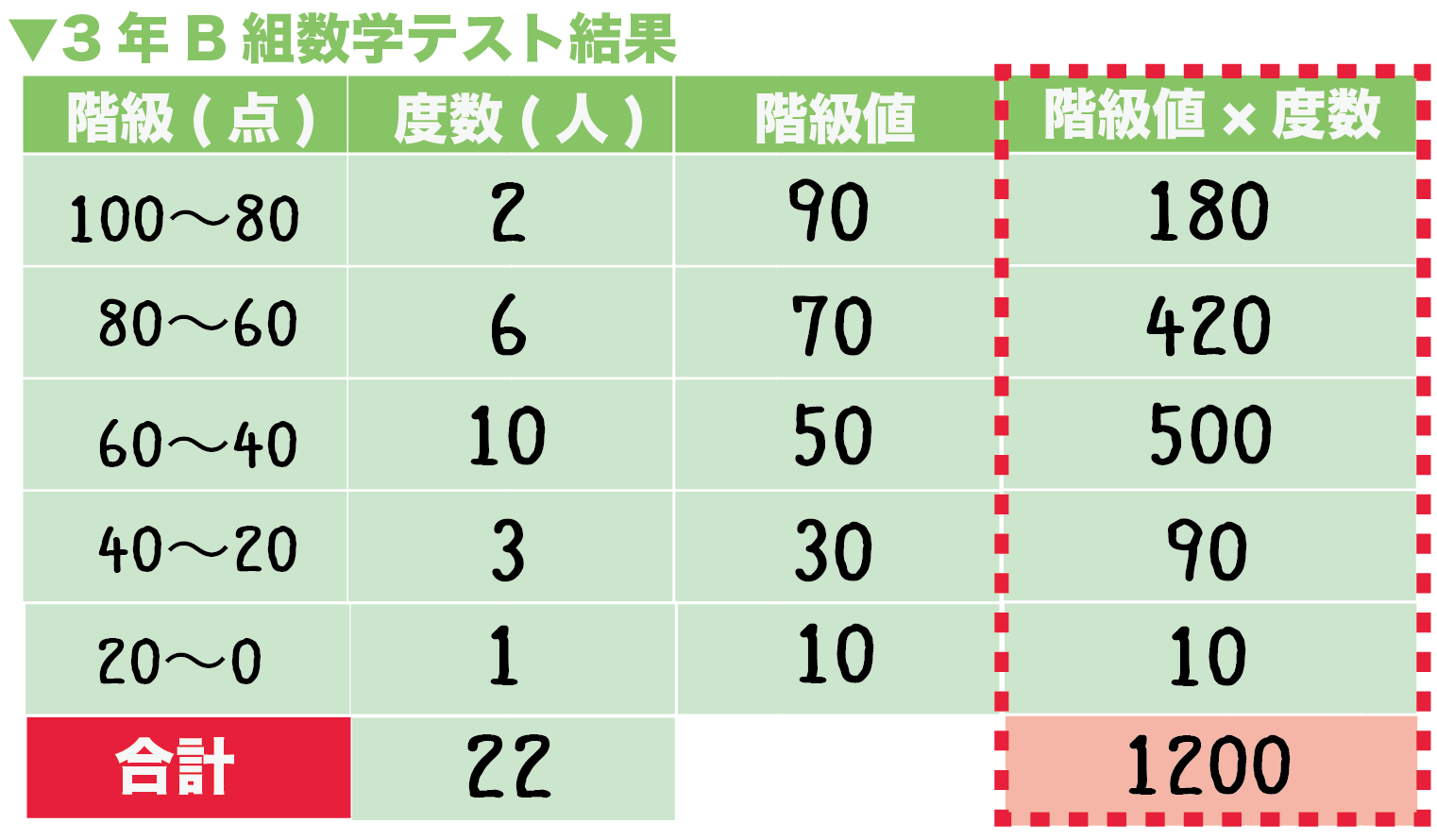
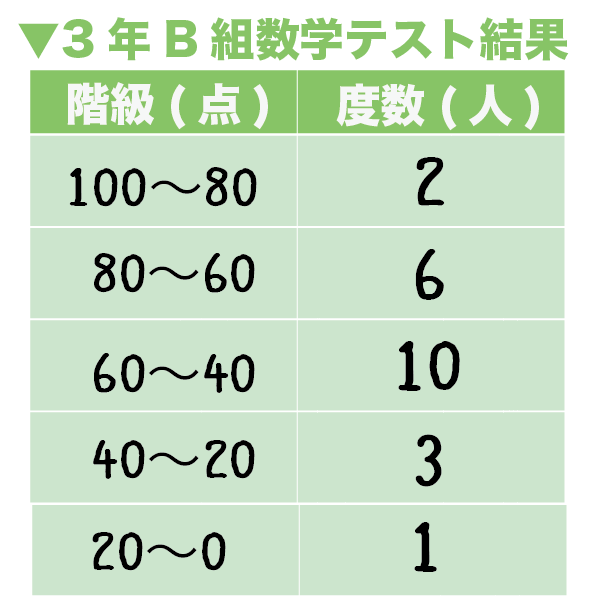
D 資料の活用 ⑴ イ 学習指導要領における領域・内容 課題の見られた問題の概要と結果 あれ?平均値なのに245 cmの あたりがへこんでいるよ。 そうだね。230 cmも高いよ。 グラフには2つの山があ平均値 = 値の合計 資料の個数 度数分布表から平均を求める場合 個々の資料の値がわからないので各階級に入っている資料の値は すべて 階級値 とみなす。 やり方 各階級の階級値を出す。 各階級で 階級値 × 度数 を計算する ②の結果をすべて加える第1学年 数学科学習指導案 1 単元名 資料の散らばりと代表値 2 単元の目標 ・資料を度数分布表やヒストグラムに整理したり、代表値や範囲などを用いたりして、資料の傾向や特徴 をとらえ意欲的に数学を問題の解決に活用しようとしている。



中学数学資料の活用答えが イ なのですが 最頻値を含む階級の度数が多い Yahoo 知恵袋




中1数学 資料の整理 度数分布表から最頻値を求める Youtube
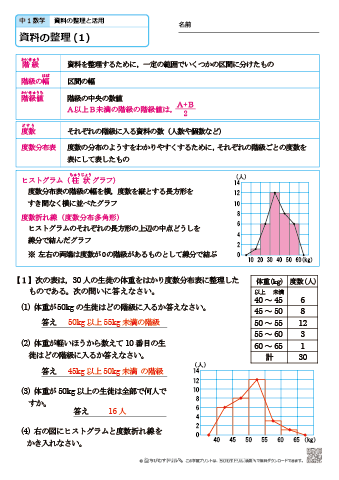
別紙資料参照(指導案綴り最終ページ)に掲載 Ⅴ 本時の学習 1 本時の目標 目的に応じて資料を整理し,ヒストグラムや範囲,代表値(平均値,メジアン,モード)などか ら資料の傾向を読み取り,自分の考えを説明することができる。第1学年 7 資料の活用 数学的な思考力・判断力・表現力を育む問題解答 年 組 号 氏名 練習問題③ (1) 0 m以上250 m未満の階級 ポイント 中央値は,大きい順に並べた中央の値だね。 この資料は偶数だから,25 番目と26 番目平均値は値の合計をデータの数で割った値です。 資料の値の合計は、=300 これを人で割ると、300÷=1510 この資料の平均値は 1510円 です。 しかし資料を見ると多くの子は平均値よりもお




中学数学 3分でわかる 階級値 ってなに Qikeru 学びを楽しくわかりやすく



Kyozai Db Fz Ocha Ac Jp Downloadpdfdisp 525
度数分布表における平均値、度数、相対度数の求め方を理解しておく。 数学用語(平均値、中央値、最頻値、階級、相対度数、幅)の理解。 度数分布表を用いた問題の出題が最も多い。 他県では、2つのヒストグラムや度数分布表の比較の問題が多く出題されています。平均値 平均値=〈(階級値×度数)の和 〉÷ 全体 確認 中1数学平均値 (注1)階級値とは、階級の幅の両サイドの数字を足して÷2 (例) 145cm以上~150cm未満 であれば、階級値は、(145+150)÷2 資料の活用の練習問題代表値 資料の値全体を1つの値で代表させ、これを基準にして、ものごとを考え たり判断したりすることがある。このようなとき、資料の値全体を代表す る値のこと。 平均値 平均値= 資料の個数 中央値




高校受験対策 資料の活用 最頻値と平均値 の問題 動画 19ch



資料の活用の問題で 中央値 最頻値 平均値の3つの問題の解き方教えて Yahoo 知恵袋
資料の活用では平均値の勘違いを確認 資料の活用では、たとえば「平均値」に注意が必要。平均点や平均年収など「平均 」と言われると「そういう人が多い」と感じますが、数学的には誤りだからです。 例で考えてみましょう。 つまり、階級値は3点ということになります。 ここで1つ注意点! 度数分布表から最頻値を求める場合、間違って度数の数を答えてしまう人がいます。 今回の資料であれば、9ですね。 これは大間違い!! 最頻値というのは、あくまで データの値 のことです。数学 統計関係部分抜粋 第3節 各学年の内容 第1学年 D 資料の活用 (1) 目的に応じて資料を収集し,コンピュータを用いたりするなどして表やグラフに整理 し,代表値や資料の散らばりに着目してその資料の傾向を読み取ることができるように する。




中学1年生 数学 資料の整理 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



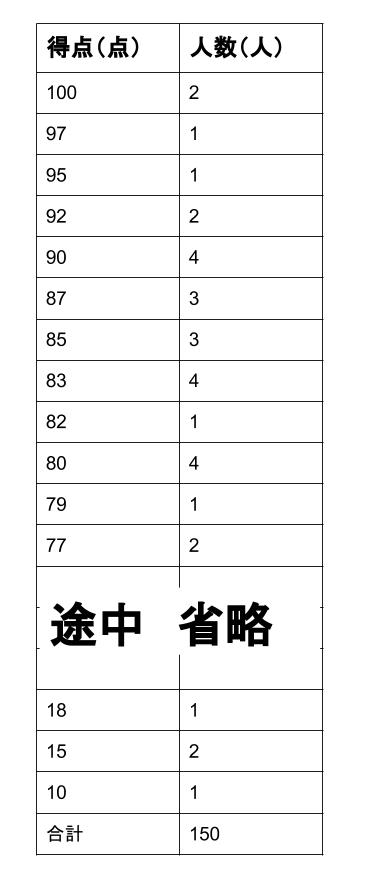
度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく
数 学 的 な 見 方 目的に応じて、度数分布表やヒストグラムに整理したり、代表値(平均値、中央値、や考え方 最頻値)や相対度数を求めたりして、資料の傾向を読み取り、説明することができる。数 学 的 な 表 現 資料を度数分布表やヒストグラムに表したり、資料の範囲や代表値(平均値、中央・処理 値、最頻値)、相対度数を求めたりすることができる。5月29 日(火) 第1時 第1学年c 組 数学科学習指導案 授業者 師 岡 洋 輔 1 題材名 資料の整理と活用 2 題材について (1) 題材観 小学校算数科では,統計的な問題解決の方法を知るとともに,棒グラフ,折れ数学では「資料のちらばりと代表値」、第3学年の数学 では「標本調査」を新たに扱うこととなった。新しい 学習指導要領において、前出の2つと第2学年の「確 率」と合わせて「資料の活用」としてまと




中学数学 資料の散らばりと代表値




度数分布表から平均値を求める 中学1年の数学 身勝手な主張
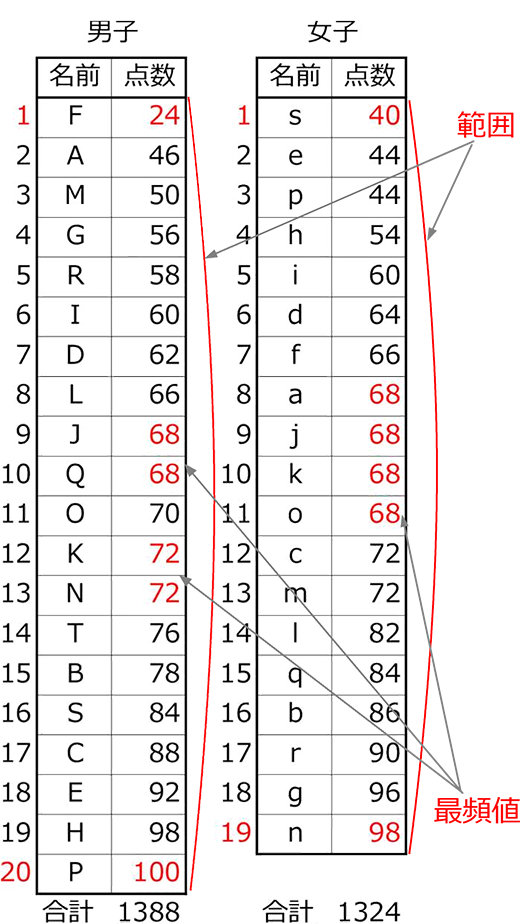
単元「資料の活用」の小単元「代表値と散らばり」(4時間)における数学的活動を取り入れた授業モデルです。 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 ・資料の平均値、中央値、最頻値を求めることができる。代表値には 「平均値」「中央値」「最頻値」「範囲」 などがあります. 「真理は1つだけでなければならない」などと決めつけてはいけません.どの代表値も長所短所があり,各自が資料を使って分析したいときに,ねらいを実現するために一番適した第1学年 資料の分析と活用 「資料の活用」 題材は,平成24年度の全国学力・学習状況調査のスキージャンプの問題をアレンジし,平均値や最頻値が等しくなるように仕上げたものである。 より遠くへ飛びそうな飛行機を選択する場面で,資料の傾向を



Q Tbn And9gcrucc9oonrnsr8xt7hwgg24wwhri7 M4v0tilyyttjwqnmgepnl Usqp Cau



中学数学 度数分布表 ヒストグラム 中学数学の無料オンライン学習サイトchu Su
平均値= {(階級値)×(度数)}の合計 度数の合計 = 960 =48 (cm) 答 48 cm 考え方 45 cm 以上 50 cm 未満の階級値 47 5 cm を仮の平均とする。 平均値=仮の平均+ {(階級値-仮の平均)×(度数)}の合計 度数の合計 解き方 475+資料の値全体を1つの値で代表させ、これを基準にして、ものごとを考えたり判断したりすること があります。このようなとき、資料の値全体を代表する値を代表値といいます。 代表値には ①平均値 ②中央値(メジアン) ③最頻値 さいひんち (モード平均値=資料の値の合計 ÷ 資料の個数 平 均 値 = 資 料 の 値 の 合 計 ÷ 資 料 の 個 数




中学数学 資料の散らばりと代表値
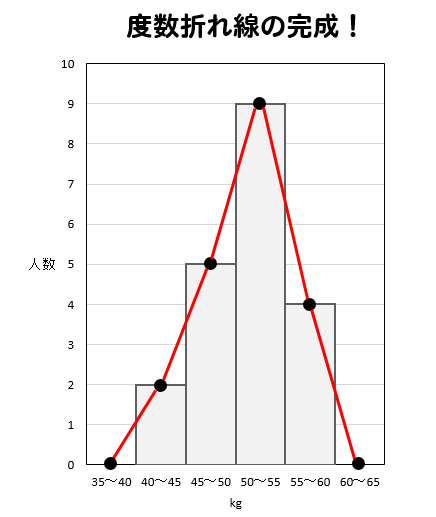



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ
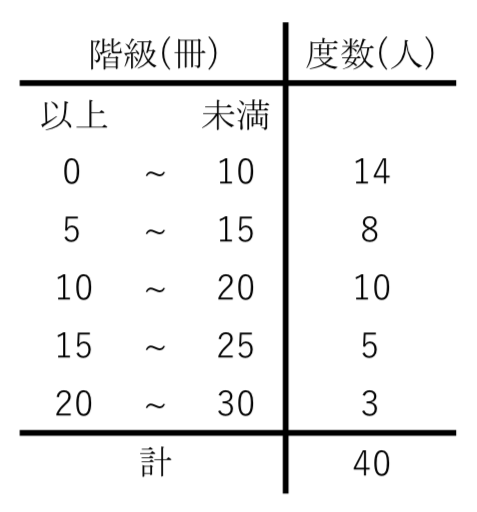



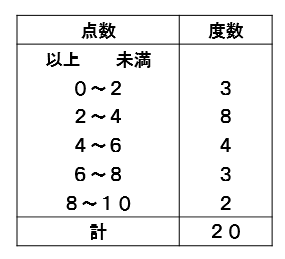
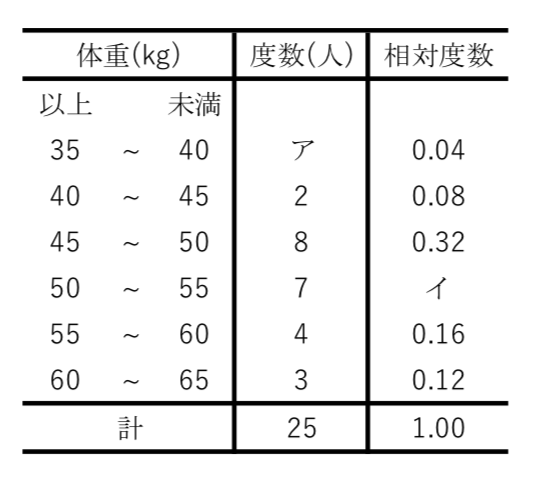
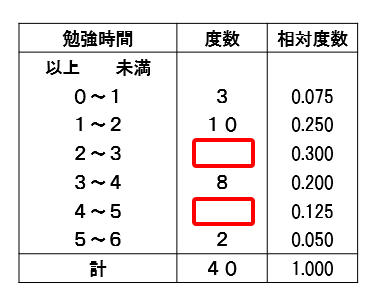
度数分布表から相対度数を求める 苦手な数学を簡単に



Q Tbn And9gct9g81v6fbuxe2zy40zobgjz7pv4jyf9dpik7xrlwfhfckmjg0k Usqp Cau



中学数学 資料の散らばりと代表値




中1 資料の活用 代表値 平均値 中央値 メジアン 最頻値 モード 最も使える中学数学範囲 デジタル板書データ リクエスト動画 Youtube




中学数学 資料の分析と活用 資料の整理 問題まとめ集 全国公立高校過去問解説集 わかりやすさに徹底的にこだわっています 教育 学習 受験 自宅でできる受験対策ショップ ワカルー Wakaru




相対度数の意味と計算方法 数学fun



フレッシュ 平均 値 求め 方 中学



1




中1 数学 中1 87 代表値と散らばり Youtube




中1数学 相対度数の求め方 例題編 映像授業のtry It トライイット




世界一わかりやすい数学問題集中1 7章 資料の活用



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




資料の活用 中1数学 中3総合a対策 しおちゃんの元氣アップ ココロのサプリ



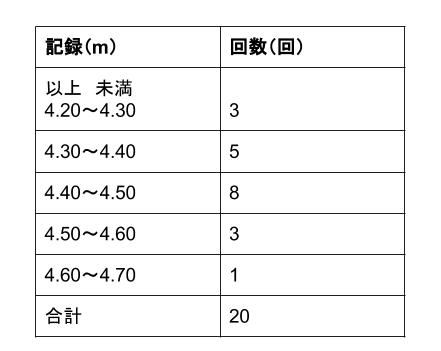
度数分布表を完成させよう 求め方は決まっている 苦手な数学を簡単に
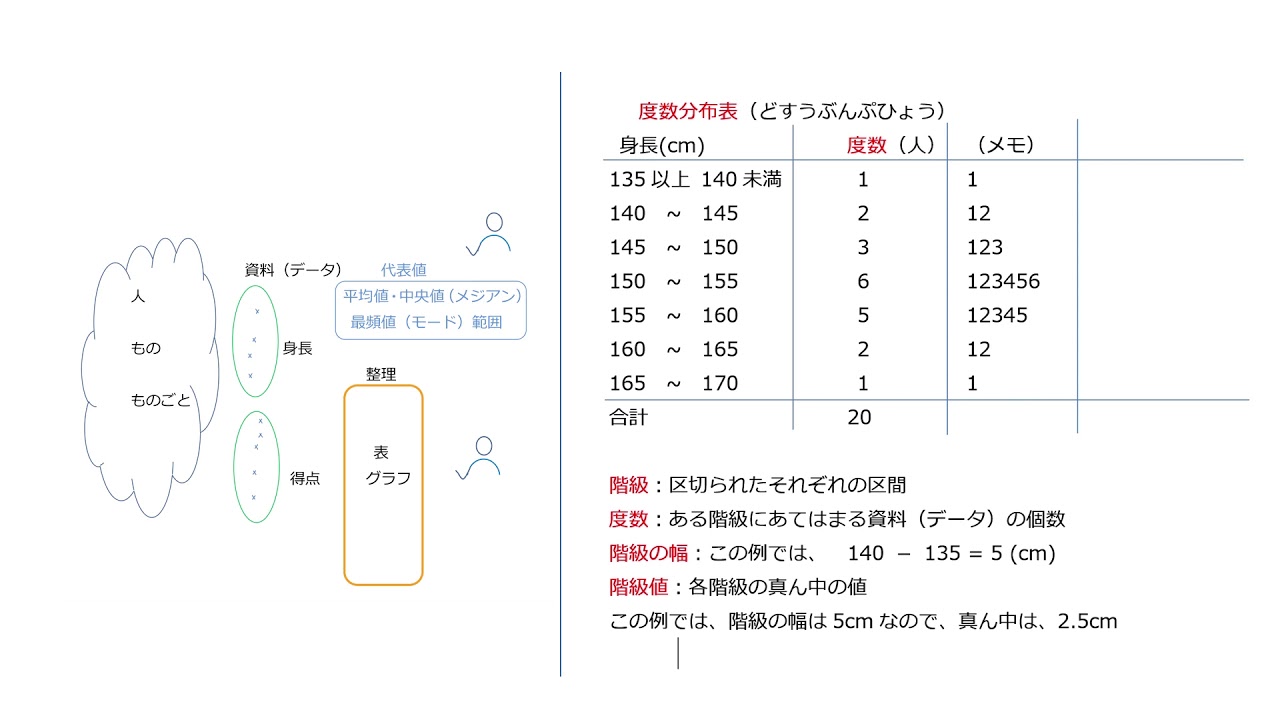



中学1年 資料の整理と活用 3 度数分布表 階級 階級値 生のデータからと度数分布表からの平均値の求め方 比較 数学を学ぶあなたを応援したいという気持ちで 授業のようにていねいに説明していきます Youtube



平均値と階級値について 苦手な数学を簡単に



無料 中1数学 基本問題 問題プリント 資料の活用2 近似値 145



無料 中1数学 基本問題 解答プリント 資料の活用2 近似値 145




中学数学 中央値 メジアン の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中1 数字 資料の活用 絶対攻略 中学生 数学のノート Clear




資料の活用 中学生 数学のノート Clear




中学数学 最頻値 モード の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




中1数学 平均値 と 中央値 練習編 映像授業のtry It トライイット




中1数学 資料の活用 平均値の求め方 Youtube
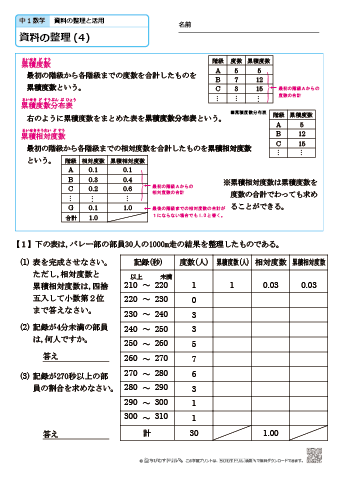



中学1年生 数学 資料の整理 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
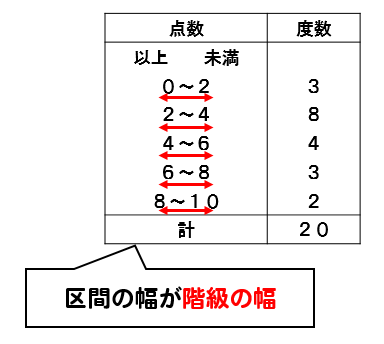



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ



2




全国学力調査 埼玉県の中3ができない数学の内容は 2 ブログ アビット




中1数学 資料の散らばりと代表値 まとめ 中学生 数学のノート Clear




中1数学 資料の活用のポイント練習問題



授業実践記録 数学 資料の活用 啓林館



中学数学 資料の散らばりと代表値



資料整理の用語 中学から数学だいすき




中学数学 資料の散らばりと代表値



中学数学 代表値 平均値 中学数学の無料オンライン学習サイトchu Su



中1数学 中央値の求め方はこれでバッチリ 偶数 奇数の場合をそれぞれ解説 数スタ



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ



至急 数学の資料の活用で質問です 下の図で 6 5秒以上7 0秒未満の階 Yahoo 知恵袋




世界一わかりやすい数学問題集中1 7章 資料の活用



1




中1 数学 資料の整理4 平均値と中央値 12分 Youtube



Http Toro J Saitama City Ed Jp Kadai 2nenn Kyouka 2suugaku 2nennsiryou3 Pdf




度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




受験対策 数学 資料の活用 Youtube



中学1年生 数学 資料の整理 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学数学 資料の分析と活用 資料の整理 問題まとめ集 全国公立高校過去問解説集 わかりやすさに徹底的にこだわっています 教育 学習 受験 自宅でできる受験対策ショップ ワカルー Wakaru



無料 中1数学 標準問題 解答プリント 145 資料の活用2 近似値



度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




國一 Junior High数学的数学 7章 資料の分析と活用 筆記 Clear




中1資料の活用 中学生 数学のノート Clear



無料 中1数学 基本解説 問題プリント 資料の活用2 近似値 145




中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




資料のちらばりと代表値 度数分布表からの平均値の求め方 中学数学 定期テスト対策サイト




中学数学 資料の散らばりと代表値



度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく



Www Chuo Tky Ed Jp Ginza Jh Resources Content 0513 Pdf



中学校数学 資料の活用 で学ぶ 中央値について質問です 資料が Yahoo 知恵袋
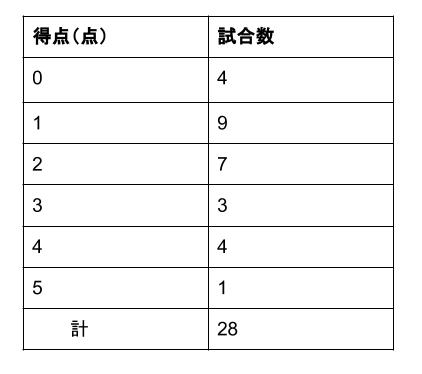



中学数学 代表値 最頻値 中学数学の無料オンライン学習サイトchu Su




中学数学 最頻値 モード の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




中学数学 資料の散らばりと代表値




中学数学 資料の散らばりと代表値



中1数学 発展 応用問題プリント 資料の活用1 度数分布表 144
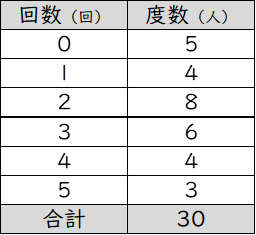



中1数学 資料の整理のポイントと定期テスト予想問題 Pikuu
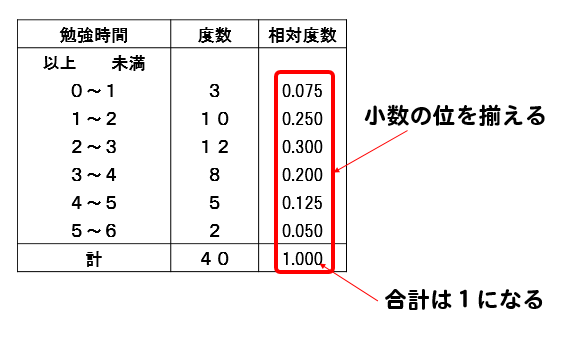



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




授業実践記録 数学 資料の活用 啓林館




中1 数字 資料の活用 絶対攻略 中学生 数学のノート Clear
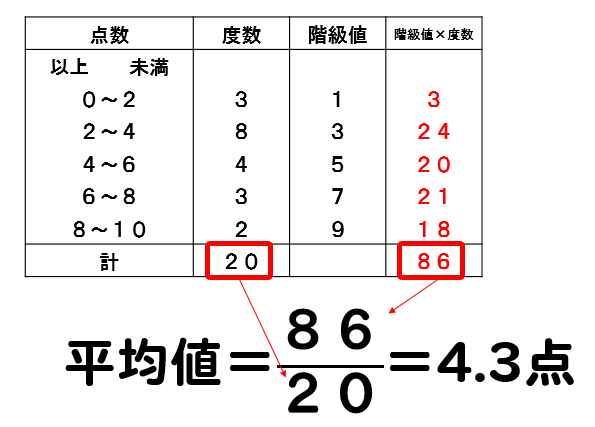



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




中1数学 資料の活用のポイント練習問題




代表値 平均値 中央値 最頻値 の意味と違い 数学fun




中1数学 平均値 と 中央値 練習編 映像授業のtry It トライイット
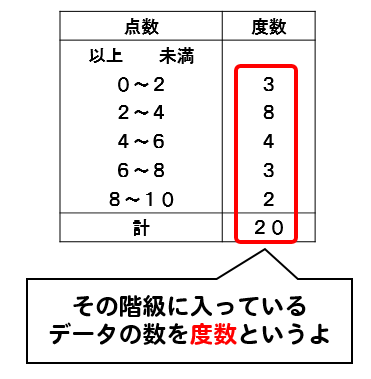



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




中1 資料の整理 中学生 数学のノート Clear




中1数学 資料の活用 平均値の求め方 Youtube



Www Nichibun G Co Jp Library E Other C Sugaku Data Katsuyou Shido Pdf
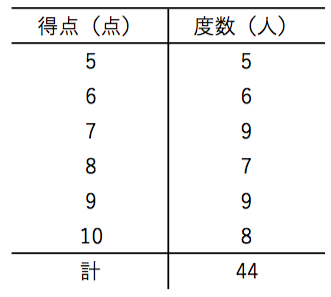



平均値について 苦手な数学を簡単に
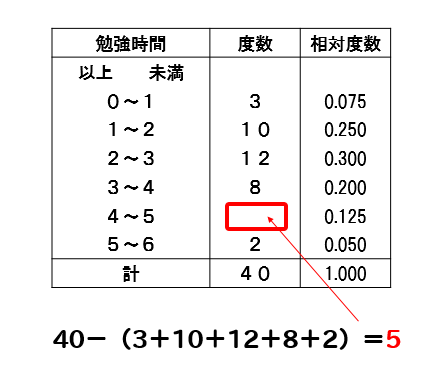



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




度数分布表から平均値を求める 中学1年の数学 身勝手な主張




中1数学 資料の整理のポイントと定期テスト予想問題 Pikuu




75 中学 数学 中央 値 壁紙 配布
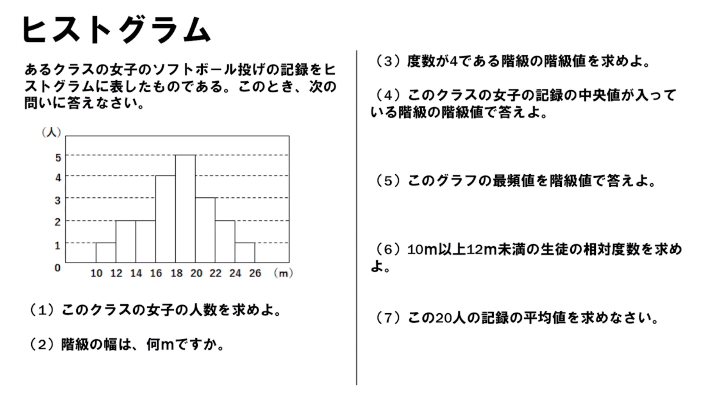



中1数学 資料の整理のポイントと定期テスト予想問題 Pikuu




フレッシュ 平均 値 求め 方 中学




中学数学 3つの代表値の求め方 Qikeru 学びを楽しくわかりやすく




代表値の応用問題 教遊者
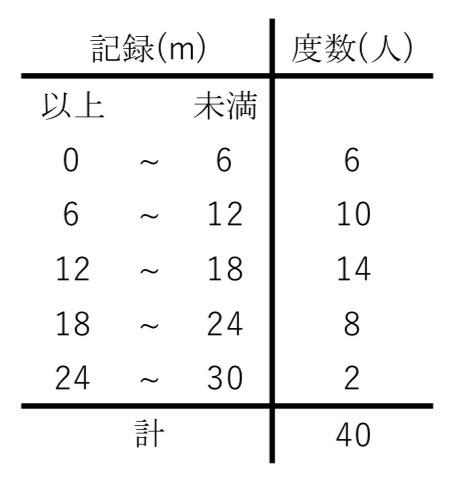



度数分布表から平均値と最頻値を求める 苦手な数学を簡単に



無料 中1数学 発展問題 解答プリント 資料の活用2 平均 相関




資料の分析と活用 まとめ集 全国公立高校過去問解説集が完成しました 恋する高校受験




中学1年生 数学 資料の整理 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中1数学 最頻値 と 階級値 練習編 映像授業のtry It トライイット



0 件のコメント:
コメントを投稿